I was reading in a book about civil engineers determining rail curvature. I recall that a 100 foot rope or chain was stretched across the curve's inside rail, then I believe a perpendicular measurement from the cord's center to the rail. What I don't remember is how the curve or radius was then determined i.e. formula, table, chart etc. for field crews to verify the curvature or radius.
Replies sorted oldest to newest
I think the railroads refer to curvature in degrees.
Rusty
Rusty Traque posted:I think the railroads refer to curvature in degrees.
Rusty
Correct. For example, a 1 degree curve would be be VERY high speed curve, while a 10 degree curve is VERY sharp, and would have a speed restriction of about 15 MPH or less.
Simply Google "RR track curvature" and there is a wealth of information provided.
Degrees down to the minutes. So many minutes of turn per foot. I don't recall the formulas, but something like that.
I think this explains how the 100' tape was used in calculating the degree of curvature on railroads, but is way beyond my pay grade  !
!
Degree of Curvature
 A circular curve is often specified by its radius. A small circle is easily laid out by using the radius. In a mathematical sense, the curvature is the reciprocal of the radius, so that a smaller curvature implies a large radius. A curve of large radius, as for a railway, cannot be laid out by using the radius directly. We will see how the problem of laying out a curve of large radius is solved. In American railway practice, the radius is not normally used for specifying a curve. Instead, a number called the degree of curvature is used. This is indeed a curvature, since a larger value means a smaller radius. The reason for this choice is to facilitate the computations necessary to lay out a curve with surveying instruments, a transit and a 100-ft engineer's tape. It is more convenient to choose round values of the degree of curvature, rather than round values for the radius, for then the transit settings can often be calculated mentally. A curve begins at the P.C., or point of curvature, and extends to the P.T., or point of tangency. The important quantities in a circular curve are illustrated above.
A circular curve is often specified by its radius. A small circle is easily laid out by using the radius. In a mathematical sense, the curvature is the reciprocal of the radius, so that a smaller curvature implies a large radius. A curve of large radius, as for a railway, cannot be laid out by using the radius directly. We will see how the problem of laying out a curve of large radius is solved. In American railway practice, the radius is not normally used for specifying a curve. Instead, a number called the degree of curvature is used. This is indeed a curvature, since a larger value means a smaller radius. The reason for this choice is to facilitate the computations necessary to lay out a curve with surveying instruments, a transit and a 100-ft engineer's tape. It is more convenient to choose round values of the degree of curvature, rather than round values for the radius, for then the transit settings can often be calculated mentally. A curve begins at the P.C., or point of curvature, and extends to the P.T., or point of tangency. The important quantities in a circular curve are illustrated above.
 The degree of curvature is customarily defined in the United States as the central angle D subtended by a chord of 100 feet. The reason for the choice of the chord rather than the actual length of circumference is that the chord can be measured easily and directly simply by stretching the tape between its ends. A railway is laid out in lengths called stations of one tape length, or 100 feet. This continues through curves, so that the length is always the length of a series of straight lines that can be directly measured. The difference between this length, and the actual length following the curves, is inconsequential, while the use of the polygonal length simplifies the calculations and measurements greatly.
The degree of curvature is customarily defined in the United States as the central angle D subtended by a chord of 100 feet. The reason for the choice of the chord rather than the actual length of circumference is that the chord can be measured easily and directly simply by stretching the tape between its ends. A railway is laid out in lengths called stations of one tape length, or 100 feet. This continues through curves, so that the length is always the length of a series of straight lines that can be directly measured. The difference between this length, and the actual length following the curves, is inconsequential, while the use of the polygonal length simplifies the calculations and measurements greatly.
The relation between the central angle d and the length c of a chord is simply R sin(d/2) = c/2, or R = c/(2 sin d/2). When c = 100, this becomes R = 50/sin D/2, where D is the degree of curvature. Since sin D/2 is approximately D/2, when D is expressed in radians, we have approximately that R = 5729.65/D, or R = 5730/D. Accurate values of R should be calculated using the sine. For example, a 2° curve has R = 2864.93 (accurate), while 5730/D = 2865 ft.
If some other value and length unit are chosen, simply replace 100 by the new value. In the metric system, 20 meters is generally used as the station interval instead of 100 ft, though stations are numbered as multiples of 10 m, and these equations are modified accordingly. With a 20 m chord, R = 1146/D m,or about 3760/D ft. Of course, a given curve has different degrees of curvature in the two systems. There are several methods of defining degree of curvature for metric curves. D may be the central angle for a chord of 10 m instead of 20 m.
The deflection from the tangent for a chord of length c is half the central angle, or δ = d/2. This is a general rule, so additional 100 ft chords just increase the deflection angle by D/2. Therefore, it is very easy to find the deflection angles if a round value is chosen for D, and usually easy to set them off on the instrument. For example, if a curve begins at station 20+34.0 and ends at station 28+77.3, the first subchord is 100 - 34.0 = 66.0 ft to station 21, then 7 100 ft chords, and finally a subchord of 77.3 ft. The deflection angle from the P.C. to the P.T. for a 2° curve is 0.660 + 7 x 1.0 + 0.773 = 8.433 °, or 8° 26'. I have used the approximate relation δ = (c/100)(D/2) to find the deflection angles for the subchords.
The long chord C from P.C. to P.T. is a valuable check, easily determined with modern distance-measuring equipment. It is C = 2R sin (I/2), where I the total central angle. For the example, C = 2(2864.93)sin(8.433) = 840.32 ft. The length of the curve, by stations, is 843.30 ft. This figure can be checked by actual measurements in the field. The actual arc length of the curve is (2864.93)(0.29437) = 843.34 ft. Note that this is the arc length on the centre line; for the rails, use R ± g/2, where g = 4.7083 ft = 56.5 in = 1435 mm for standard gauge.
Before electronic calculators, small-angle approximations and tables of logarithms were used to carry out the computations for curves. Now, things are much easier, and I write the equations in a form suitable for scientific pocket calculators, instead of using the traditional forms that use tabular values and approximations.
A 1° curve has a radius of 5729.65 feet. Curves of 1° or 2° are found on high-speed lines. A 6° curve, about the sharpest that would be generally found on a main line, has a radius of 955.37 feet. On early American railroads, some curves were as sharp as 400 ft radius, or 14.4°. Street railways have even sharper curves. The sharpest curve that can be negotiated by normal diesel locomotives is not less than 250 ft radius, or 23°. It is not difficult to apply spirals, in which the change of curvature is proportional to distance, to the ends of a circular curve. Circular curves are a good first approximation to an alignment.
The centrifugal acceleration in a curve of radius R negotiated at speed v is a = v2/R. If v is in mph, a = 2.1511v2/R = 3.754 x 10-4Dv2 ft/s2, where D is degrees of curvature. This is normal to the gravitational acceleration of 32.16 ft/s2, and the total acceleration is the vector sum of these. For comfort, a maximum ratio of a to g may be taken as 0.1 (tan-1 5.71°). The overturning speed depends on the height of the centre of gravity, and occurs when a line drawn from the centre of gravity parallel to the resultant acceleration passes through one rail. The height of the centre of gravity of American railway equipment is 10 ft or less. Taking 10 ft as the height of the centre of gravity, a/g = 0.2354 (tan-1 13/25°). Therefore, the overturning speed vo can be estimated by Dvo2 = 20,000 and the comfort speed vc by Dvc2 = 8500.
A curve may be superelevated by an amount s so that the resultant acceleration is more normal to the track. Exact compensation occurs only for one speed, of course. This angle of bank is given by tan θ = a/g = 1.167 x 10-5Dv2, and sin θ = s/gauge. Consider a 2° curve. For v = 60 mph, tan θ = 0.08404, sin θ = 0.08375 and s = 4.73 in. If the speed is greater than this, there will be an unbalanced acceleration, which will have a ratio of a/g of 0.1 at a speed v' given by 0.1 = 1.167 x 10-5D(v'2 - v2), or v' = 89 mph. The overturning speed on this curve is given by (0.2354 + 0.08404) = (1.167 x10-5)Dv2, or v = 117 mph. Note that a large superelevation will cause the flanges of a slow-moving train to grind the lower rail. Superelevation is generally limited to 6 to 8 in maximum.
I found this formula that seems to work:
R = radius (in feet)
D = perpendicular distance from center of 100' chain/rope to rail (in feet)
R = D/2 + 1250/D
This formula is only for a chain/rope of 100'. The more general formula for a chain of any length is as follows:
R = D/2 + (length of chain)*(length of chain)/8D
Here is the most direct explanation I can give for specification of railroad curves in degrees rather than radius. First, the reason it is done this way is because, in building a railroad, the center of a curve may not be accessible to a surveyor. For example, it may be at the top of a mountain or in a lake.
The curve specification (in degrees) is just the number of degrees of direction change in a (chord) distance of 100 feet. If I walk 100 feet (in a straight line between two locations on the track), the direction of the track has changed by the number of degrees that describes the curvature.
How many degrees are there in a circle? Answer = 360. Once I know the "degrees of curvature," (say 6) I can divide 360 by the "degrees of curvature," which will tell me how many 100-foot chords it takes to go all the way around the circle (in this case 60). That number tells me the (approximate) circumference of the circle which is 60 times 100 = 6000 feet. Then, circumference equals two times pi (3.1416) times the radius (R). If I solve this equation for radius (R), I get radius = circumference / two times pi = 6000 / (6.2832) = 954.9 feet.
Doing it as I described above is approximate because a 100 foot distance along the chord is not exactly equal to the distance along the curve. The exact answer for the radius is:
Radius = 100 /(2 * sine (degrees /2))
From the formula, the exact numerical answer in this case would be 955.4 feet.
MELGAR
Guys, There is a much easier method for measuring the degree of curvature in the field, on the track. And this information is direct from the Federal Railway Administration Track Safety Standards, and also numerous archival track maintenance manuals. My railroad background was initially in Maintenance of Way and later operations on both Class 1's and later short lines.
Most railroads have a transition from tangent (straight) track into full curvature known as a spiral, where the curvature and superelevation gradually increase from the tangent until the full curvature is reached, to allow the rail wheels to adjust gradually to full curvature.
The measuring method is to use a string of a measurement of 62 feet, with the center of the string marked at 31 feet, stretched along the inner or "gauge" side of the high rail of the curve. An ordinary tape or ruler held in contact with the gauge side of the rail at the 31 foot mark gives the degree of curvature in even inches, i.e., 3 inches=3 degrees. It follows that each one-half inch additional is 30 minutes, one-quarter inch 15 minutes, and so on. So 3-3/4" equals 3 degrees,45 minutes curve.
While this method seems simple, it has been followed down through the years, probably since the beginning of railroads. It is easier, surely, than using a transit and surveyor's chain would be. It is also firmly grounded in geometry, which I won't explore here. Those of you of the metric persuasion, I don't have the conversions at hand at the moment.
I hope this wasn't "as clear as mud"! Don Francis
To provide a little context here, on the real railroad at 12" to the foot scale, on a branch or in the yard you might see 15 or 20-degree curves. These are VERY sharp curves and not all rail equipment will go around a 20-degree curve. 5 to 10 mph is an appropriate speed for these very tight curves. However, a 20-degree curve is an O-144 curve!
On a railroad main line, 2 to 4 degree curves are common and would not require any speed restriction to go around them. 5 and 6 degree curves are sharp enough to require speed restrictions. A 5-degree curve is an O-575 curve! Think you've got room for that?
The world-famous Horseshoe Curve, on the ex-PRR just west of Altoona, PA, is a 9-degree curve with a 25 mph speed limit. That's an O-320 curve.
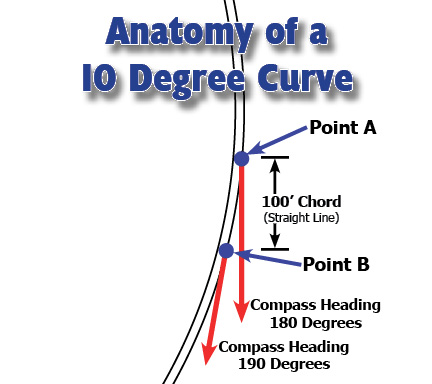
Here's a somewhat simplified diagram showing how "Degrees of Curvature" are measured.
Attachments
Thanks Rich, I learned something. I need to buy a stadium with no seats to set up my trains to be realistic.
Happy New Year
Rich Melvin posted:
On a railroad main line, 2 to 4 degree curves are common and would not require any speed restriction to go around them. 5 and 6 degree curves are sharp enough to require speed restrictions. A 5-degree curve is an O-575 curve! Think you've got room for that?
The world-famous Horseshoe Curve, on the ex-PRR just west of Altoona, PA, is a 9-degree curve with a 25 mph speed limit. That's an O-320 curve.
Lets see. O-575 would be a comfortable 50 foot wide room, O-320 wold be about a 30 foot wide to allow some walk around room.
I start saving my pennies and see what an architect can come up with for 50 by 100+ foot home. ![]() Well, could have basement walls with lots of large windows be outer house edges and then have bedrooms, kitchen, living spaces inside layout rails. In effect, layout outside home rather than layout inside home, similar to those outdoor G gauge layouts
Well, could have basement walls with lots of large windows be outer house edges and then have bedrooms, kitchen, living spaces inside layout rails. In effect, layout outside home rather than layout inside home, similar to those outdoor G gauge layouts
Rich Melvin posted:To provide a little context here, on the real railroad at 12" to the foot scale, on a branch or in the yard you might see 15 or 20-degree curves. These are VERY sharp curves and not all rail equipment will go around a 20-degree curve. 5 to 10 mph is an appropriate speed for these very tight curves. However, a 20-degree curve is an O-144 curve!
On a railroad main line, 2 to 4 degree curves are common and would not require any speed restriction to go around them. 5 and 6 degree curves are sharp enough to require speed restrictions. A 5-degree curve is an O-575 curve! Think you've got room for that?
The world-famous Horseshoe Curve, on the ex-PRR just west of Altoona, PA, is a 9-degree curve with a 25 mph speed limit. That's an O-320 curve.
Here's a somewhat simplified diagram showing how "Degrees of Curvature" are measured.
Many years ago while doing high speed passenger cost studies for FRA and a few states, I worked with some railway engineers who had some basic specs for curve speeds. Limits were related not only the degree of curvature but also to the amount of super-elevation. One set of numbers that remains in my head is that the maximum curvature for 80 mph was 2 degrees with six inch super-elevation and two inches unbalance.
From that, we know that you could not have taken four degree curves without speed restriction on normal passenger service track. From 1947 until recently, the maximum passenger train speed on lines without cab signalling or automatic train stop was 80. That was the normal speed on most passenger railroads except on line segments with numerous curves exceeding two degrees. Six inches was normal super-elevation where passenger trains operated. Unbalance was the extent to which super-elevation did not fully offset centrifugal force. I don't recall whether the accepted amount was two or three inches. This was essentially a matter of how much sideways force was acceptable for passengers.
Thank you for this discussion. I often wondered why curves were only listed in degrees: there had to be another value for the size of the curve to be determined. Not only were my original questions answered but other variables such as easements, super elevation and transition tracks discussed.