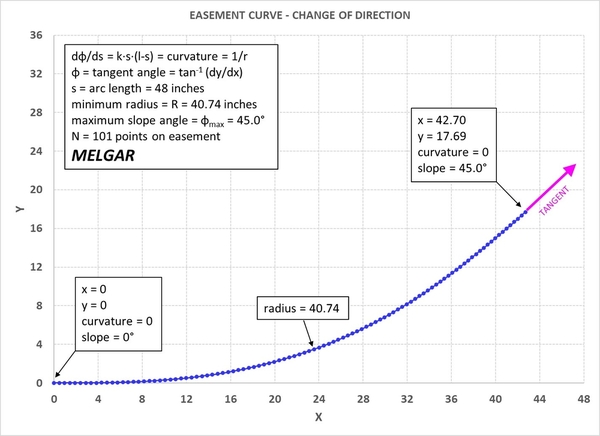
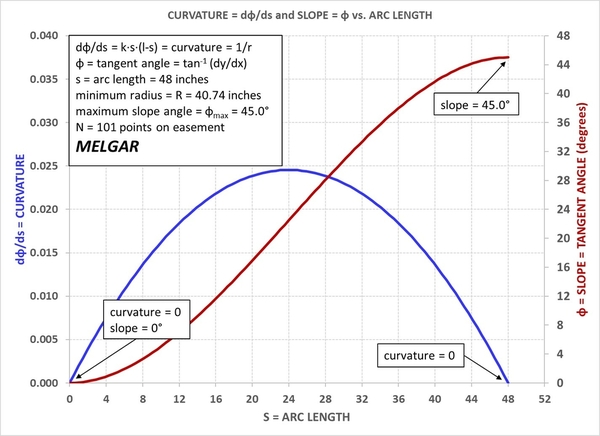
In planning my layout, I ran down the easement rabbit hole in some depth. The following discussion is based on the semi-empirical method of easement curve layout described in John Armstrong's "Track Planning for Realistic Operation". The process is set forth in Figure 8-8 of the original 1963 edition. It is apparent that the table in Armstrong's figure was derived using the equations set forth in James Glover's "Transition Curves for Railways", published in the Proceedings of the Institution of Civil Engineers (UK) in 1900 (and downloadable online). The Glover paper appears to have been the basis for prototype curve easement calculations for a hundred years.
What Armstrong's table does not state is the angular sector assumed in calculating the easement parameters. Using Glover's equations, Armstrong's table can be completed as follows (with some 1/16" difference because I'm not using a slide rule):
| Armstrong Easement Table, Sectors & Total Diameter Added |
| Diameter | Radius | Sector | Length L | Shift x | Total d |
| (in.) | (in.) | (deg.) | (in.) | (in.) | (in.) |
| 36 | 18 | 19.1 | 12 | 5/16 | 36 11/16 |
| 48 | 24 | 19.1 | 16 | 7/16 | 48 7/8 |
| 60 | 30 | 17.2 | 18 | 7/16 | 60 7/8 |
| 64 | 32 | 17.9 | 20 | 1/2 | 65 1/16 |
| 84 | 42 | 17.05 | 25 | 5/8 | 85 1/4 |
| 108 | 54 | 15.9 | 30 | 11/16 | 109 3/8 |
"Total d" is the total effective diameter of a semicircle, including easements at both ends. An O-60 semicircle with easements as defined by Armstrong would occupy 60-7/8" of space, plus tie width. From these data, it is apparent that Armstrong assumed a sector of approximately 18°. Assuming that sector and applying it to a wider range of diameters/radii, the following table results:
| Flex Track Easement Table - 18° Easement Sectors |
| Diameter | Radius | Length L | Shift x | Total d |
| (in.) | (in.) | (in.) | (in.) | (in.) |
| 36 | 18 | 11 5/16 | 5/16 | 36 9/16 |
| 42 | 21 | 13 3/16 | 3/8 | 42 6/8 |
| 48 | 24 | 15 1/16 | 3/8 | 48 6/8 |
| 54 | 27 | 16 15/16 | 7/16 | 54 14/16 |
| 64 | 32 | 20 1/8 | 1/2 | 65 |
| 72 | 36 | 22 5/8 | 9/16 | 73 1/8 |
| 80 | 40 | 25 1/8 | 11/16 | 81 3/8 |
| 88 | 44 | 27 5/8 | 3/4 | 89 4/8 |
| 96 | 48 | 30 3/16 | 13/16 | 97 5/8 |
| 104 | 52 | 32 11/16 | 7/8 | 105 6/8 |
| 112 | 56 | 35 3/16 | 15/16 | 113 7/8 |
| 128 | 64 | 40 3/16 | 1 1/16 | 130 1/8 |
Use of sectional track fixes the sectors at different values. For example, small diameters use 8 sections per circle and 2 per quadrant, so it's impractical to use more than one fixed track section per quadrant. The transition sectors for the quadrant become half of the normal section sector, 45°. The same holds for 12 sections per circle situations, where each section defines a 30° sector, but in a quadrant one would use two fixed section and two half-sector transitions, 15° each. It should also be noted, as Glover stated in his paper, that the underlying mathematics apply for "small" sectors (though Glover doesn't define them). I assumed that "small" means sectors below 25°. So, based on sectional track, the table can be re-stated this way:
| Sectional Track - Half Section Easements <16 per Circle, Full > 12 per Circle |
| Diameter | Radius | Sections | Sector | Length L | Shift x | Total d |
| (in.) | (in.) | | (deg.) | (in.) | (in.) | (in.) |
| 31 | 15.5 | 8 | 22.5 | 12 3/16 | 3/8 | 31 13/16 |
| 36 | 18 | 8 | 22.5 | 14 1/8 | 7/16 | 36 15/16 |
| 42 | 21 | 8 | 22.5 | 16 1/2 | 9/16 | 43 1/16 |
| 48 | 24 | 12 | 15 | 12 9/16 | 1/4 | 48 9/16 |
| 54 | 27 | 12 | 15 | 14 1/8 | 5/16 | 54 5/8 |
| 72 | 36 | 16 | 22.5 | 28 1/4 | 15/16 | 73 7/8 |
| 80 | 40 | 16 | 22.5 | 31 7/16 | 1 | 82 1/16 |
| 88 | 44 | 16 | 22.5 | 34 9/16 | 1 1/8 | 90 1/4 |
| 96 | 48 | 16 | 22.5 | 37 11/16 | 1 1/4 | 98 7/16 |
| 104 | 52 | 16 | 22.5 | 40 13/16 | 1 5/16 | 106 11/16 |
| 112 | 56 | 16 | 22.5 | 44 | 1 7/16 | 114 7/8 |
| 120 | 60 | 16 | 22.5 | 47 1/8 | 1 9/16 | 123 1/16 |
| 128 | 64 | 16 | 22.5 | 50 1/4 | 1 5/8 | 131 5/16 |
At 16 sections per circle, it is also possible to use half section sectors with three fixed sections in between. However, this reduces the easement "shift" number significantly and thereby doesn't provide as gradual a transition. At the widest diameters, that may not matter much, aesthetically. It's really a matter of how much of a circle you prefer to implement with fixed sections vs. flex track.
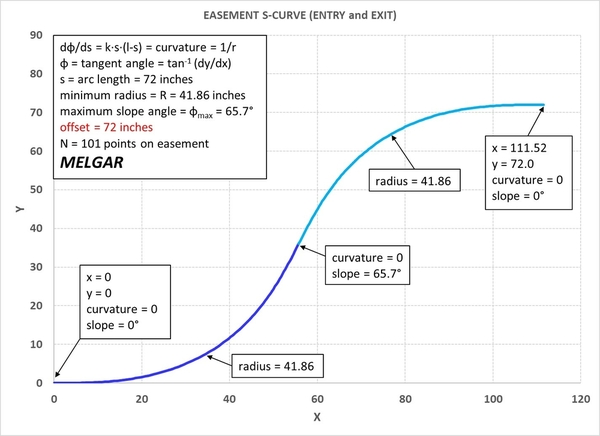
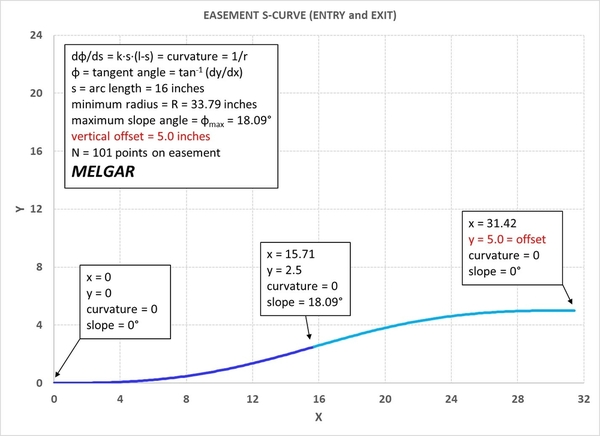
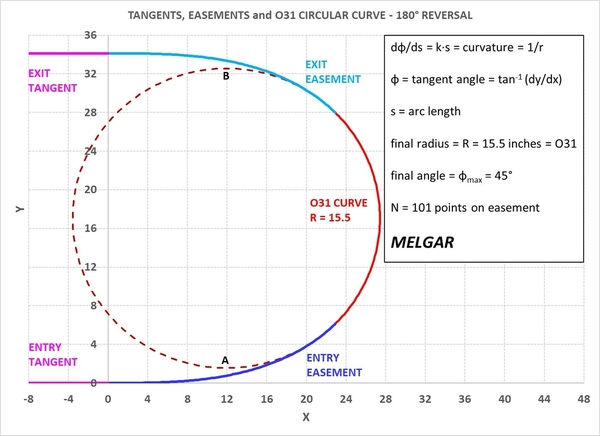
Glover's paper also recommends easing superelevation over the transition length L noted in the tables above. Using the math laid out in Glover's paper, more general situations can be analyzed, x-y coordinates of points along a transition curve defined, and so on, for the mathematically curious or compulsive. There are other formulations that can be useful in certain situations. For example, I have two horseshoe curves which are obscured in a lower level. These are implemented using continuously varying radii that go from O-72 at the horseshoe apex to O-104 nearing the (visible) edges, on the inner track. The curve was defined mathematically using a non-cubic approach.
--Karl